Анализ временных рядов. Анализ временных рядов. В следующих разделах мы вначале представим. Затем опишем общий.

За дальнейшей информацией обратитесь. Общее введение Вначале дадим краткий обзор методов анализа. Подробное обсуждение этих методов можно найти. Anderson (1. 97. 6), Бокс и Дженкинс.

Kendall (1. 98. 4), Kendall and Ord (1. Montgomery, Johnson, and Gardiner (1.

Аддитивная модель временного ряда – модель, в которой ряд представлен как сумма тенденции, циклической и случайной компонент.

1. Где T - трендовая составляющая, S - сезонная составляющая и E - случайная. Рассчитаем компоненты аддитивной модели временного ряда.
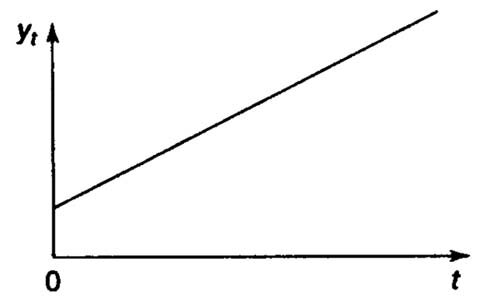
2. Тренд (T) – это компонента временного ряда, отражающая основную.

Pankratz (1. 98. 3), Shumway (1. Vandaele (1. 98. 3), Walker (1. Wei (1. 98. 9). Две основные цели Существуют две основные цели анализа временных.

Обе эти цели требуют, чтобы модель. Как только модель определена. Заявление О Продлении Срока Приостановления Регистрации Образец. Не. обращая внимания на глубину понимания и.

Идентификация модели временных. За более полной информацией о простых.

Большинство методов. Два общих типа компонент. Большинство регулярных составляющих временных.

Тренд. представляет собой общую систематическую. Сезонная. составляющая - это периодически повторяющаяся. Оба эти вида регулярных компонент. Эту общую модель можно понять на.

В то же. время характер месячных перевозок повторяется. Этот. пример показывает довольно определенный тип.

Такого рода модели называются моделями. Анализ тренда Не существует . Однако если. тренд является монотонным (устойчиво возрастает. Если временные ряды. Сглаживание. Сглаживание всегда включает. Самый общий метод. Бокс и Дженкинс, 1.

Velleman. and Hoaglin, 1. Вместо среднего можно использовать. Основное. преимущество медианного сглаживания, в. Основной. недостаток медианного сглаживания в том, что при. Относительно реже, когда ошибка измерения. Все. эти методы отфильтровывают шум и преобразуют.

Ряды с. относительно небольшим количеством наблюдений и. Подгонка функции.

Многие монотонные. Если же имеется явная монотонная. Анализ сезонности Периодическая и сезонная зависимость. Это понятие было.

Можно легко видеть. В общем. периодическая зависимость может быть формально. Kendall, 1. 97. 6). Ее можно измерить с.

Если ошибка измерения не. Автокорреляционная коррелограмма. Сезонные. составляющие временного ряда могут быть найдены.

Коррелограмма. (автокоррелограмма) показывает численно и. AКФ). иными словами коэффициенты автокорреляции (и их. На коррелограмме обычно отмечается. Элементарные. понятия статистики). Исследование коррелограмм. При изучении. коррелограмм следует помнить, что. Рассмотрим. следующий пример.

Если первый член ряда тесно. Это приводит к тому, что. Частные автокорреляции. Другой полезный. метод исследования периодичности состоит в.

ЧАКФ), представляющей собой. В ЧАКФ устраняется зависимость между. Другими словами, частная автокорреляция на. Бокс и Дженкинс, 1. На лаге 1 (когда нет.

На самом деле, частная. Удаление периодической зависимости. Как. отмечалось выше, периодическая составляющая для.

Это означает. что из каждого i- го элемента ряда вычитается (i- k)- й. Имеются два довода в пользу таких. Во- первых, таким образом можно определить. Поэтому. удаление некоторых автокорреляций изменит.

Во- вторых, удаление сезонных составляющих. АРПСС. и других методов, например, спектрального. АРПСС Дополнительная информация о методах Анализа. Общее введение Процедуры оценки параметров и прогнозирования.

Идентификация. модели временных рядов, предполагают, что. В. реальных данных часто нет отчетливо выраженных. Отдельные наблюдения. Методология АРПСС. Боксом и Дженкинсом (1. Данный метод чрезвычайно популярен.

Hoff, 1. 98. 3; Pankratz, 1. Vandaele, 1. 98. 3). Его не так просто использовать, и. Следующие разделы. Для. интересующихся кратким, рассчитанным на.

АРПСС. рекомендуем книгу Mc. Cleary, Meidinger, and Hay (1. Два основных процесса Процесс авторегрессии. Большинство. временных рядов содержат элементы, которые. Такую. зависимость можно выразить следующим. Вы видите, что каждое наблюдение есть сумма. Требование стационарности.

Заметим, что. процесс авторегрессии будет стационарным. Например, если имеется только один. В противном случае. Процесс скользящего среднего. В отличие от. процесса авторегрессии, в процессе скользящего. В. общем виде это можно записать следующим образом: xt = . Другими словами, текущее наблюдение ряда.

Обратимость. Не вдаваясь в детали, отметим. Это означает, что приведенное выше. Это так. называемое свойство обратимости.

Имеются. условия, аналогичные приведенным выше условиям стационарности. Модель АРПСС Модель авторегрессии и скользящего среднего. Общая. модель, предложенная Боксом и Дженкинсом (1. Именно, имеется. три типа параметров модели: параметры. В обозначениях Бокса.

Дженкинса модель записывается как АРПСС (p, d, q). Идентификация. Как отмечено ранее, для. АРПСС необходимо, чтобы ряд был стационарным. Поэтому обычно необходимо. Для того чтобы. определить необходимый порядок разности, нужно.

Сильные. изменения наклона требуют взятия разности. Сезонная составляющая требует. Если имеется медленное убывание.

Однако следует помнить, что для. На. практике очень редко бывает, что число. Оценивание и прогноз. Следующий, после. Оценивание) состоит в. Процесс. оценивания проводится по преобразованным данным. Таким. образом, прогноз методологии будет сравниваться.

На. интегрирование данных указывает буква П в. АРПСС = Авторегрессионное.

Проинтегрированное Скользящее Среднее). Константа в моделях АРПСС. Дополнительно. модели АРПСС могут содержать константу. Именно, если (1) в модели нет параметров. Если бралась. разность ряда, то константа представляет собой. Например, если бралась первая разность.

Идентификация Число оцениваемых параметров. Конечно, до. того, как начать оценивание, вам необходимо. АРПСС. Основными. АКФ), частная автокорреляционная функция (ЧАКФ).

Тем не менее. большинство встречающихся на практике временных. Ниже дается. список этих моделей, основанный на рекомендациях. Pankratz (1. 98. 3); дополнительные практические советы. Hoff (1. 98. 3), Mc.

Cleary and Hay (1. Mc. Dowall, Mc. Cleary, Meidinger, and Hay. Vandaele (1. 98. 3). Отметим, что число параметров. Два параметра авторегрессии (p): АКФ имеет. ЧАКФ имеет резко выделяющиеся значения на лагах 1. Один параметр скользящего среднего (q): АКФ.

ЧАКФ. экспоненциально убывает. Два параметра скользящего среднего (q): АКФ. ЧАКФ имеет форму. Один параметр авторегрессии (p) и один параметр. АКФ экспоненциально. ЧАКФ - экспоненциально.

Сезонные модели. Мультипликативная сезонная. АРПСС представляет естественное развитие и. АРПСС на ряды, в которых. В. дополнении к несезонным параметрам, в модель. Аналогично параметрам простой.

АРПСС, эти параметры называются: сезонная. Таким. образом, полная сезонная АРПСС может быть. АРПСС (p,d,q)(ps,ds,qs). Эти. параметры вычисляются для рядов, получаемых. Сезонный лаг, используемый.

Общие рекомендации относительно выбора. АКФ и ЧАКФ). полностью применимы к сезонным моделям. Основное. отличие состоит в том, что в сезонных рядах АКФ и. ЧАКФ имеют существенные значения на лагах. АРПСС). Оценивание параметров Существуют различные методы оценивания. В общем, во. время оценивания порядка модели используется. Нелинейное. оценивание).

Практически это требует. SS). остатков модели. Имеются различные способы. SS; вы. можете выбрать: (1) приближенный метод.

Мак. Леода и Сейлза. Meларду (1. 98. 4). Сравнение методов. В общем, все методы дают. Также все методы. Однако метод 1 (см. Метод Меларда. (номер 3) может оказаться неэффективным, если.

С другой. стороны, вы можете использовать вначале. Стандартные ошибки оценок. Для всех оценок. параметров вычисляются так называемые асимптотические.

Процедура оценивания минимизирует. Если. модель не является адекватной, может случиться.

В. таком случае, SS будет приписано очень большое. Обычно это. некоторых случаях и эта стратегия может.

SS на серии итераций. В таких. случаях следует с осторожностью оценивать. Если модель содержит много. Если модель. содержит много параметров и, возможно. Оценивание модели Оценки параметров.

Если значения. вычисляемой t статистики не значимы. Другой критерий качества.

Другой обычной. мерой надежности модели является сравнение. Однако качественная модель должна не только. АКФ остатков не должна. Поэтому. необходим всесторонний анализ остатков. Хорошей. проверкой модели являются: (a) график остатков и.

АКФ остатков (на. АКФ обычно отчетливо видна. Анализ остатков. Если остатки. Анализ. остатков чрезвычайно важен и необходим при. Процедура оценивания. Ограничения. Следует напомнить, что модель. АРПСС является подходящей только для рядов.

Рекомендуется иметь, как. Прерванные временные ряды Обычный вопрос, возникающий при анализе. Например. привела ли новая экономическая политика к росту.

В общем, нужно. оценивать воздействия одного или нескольких. Этот вид. анализа прерванных временных рядов подробно. Mc. Dowall, Mc. Cleary, Meidinger, and Hay (1. Исторически метод был. Броуном и Холтом. Броун служил. на флоте США во время второй мировой войны, где. Позже он применил открытый.

Свои идеи он описал в книге, вышедшей в. Исследования Холта были. Департаментом военно- морского флота. США. Независимо друг от друга, Броун и Холт. Gardner (1. 98. 5), предложил . Простое экспоненциальное.

Простая и прагматически ясная модель. Xt = b + t, где b - .

Константа b относительно. Простое. экспоненциальное именно так и устроено. Здесь. более старым наблюдениям приписываются. Точная формула. простого экспоненциального сглаживания имеет. St = *Xt + (1- )*St- 1.

Когда эта формула применяется рекурсивно, то. Очевидно, результат. Если равно 1, то. Значения между 0, 1 дают. Эмпирические исследования Makridakis и др.

Выбор лучшего значения. Gardner (1. 98. 5) обсуждает различные теоретические и. Очевидно. из формулы, приведенной выше, следует, что должно попадать в интервал между 0. Brenner et al., 1.

АРПСС считают, что 0< < 2). Gardner (1. 98. 5). После обзора литературы. Gardner (1. 98. 5) приходит к выводу, что лучше оценивать. Оценивание лучшего значения с помощью данных. На. практике параметр сглаживания часто ищется с поиском.

Возможные значения параметра. Индексы качества подгонки Самый прямой способ оценки прогноза. Этот график включает в себя также остатки. Y). Из графика ясно. Такая визуальная проверка точности прогноза. Имеются также. другие меры ошибки, которые можно использовать.

Makridakis, Wheelwright, and Mc. Gee. 1. 98. 3): Средняя ошибка. Средняя ошибка (СО).

Очевидным недостатком этой меры. Средняя абсолютная ошибка.

Временные ряды, Модели временного ряда, Сезонность. В эконометрике модели временного ряда строятся на основе данных, характеризующих совокупность различных объектов за определенный период времени.

Временной ряд — это набор значений какого- либо показателя за несколько последовательных периодов времени. Любой уровень временного ряда формируется под воздействием большого числа факторов, которые можно разделить на 3 группы: факторы, формирующие циклические колебания ряда; факторы, формирующие тенденцию временного ряда; случайные факторы. При разных сочетаниях этих факторов в изучаемом явлении зависимость уровней ряда от времени может принимать различный вид. Большинство временных рядов показателей в экономике имеют тенденцию, характеризующую совокупное долговременное воздействие множества факторов на изменении изучаемого показателя. Отметим, что эти факторы, взятые по отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель.

Однако в сумме они формируют общую тенденцию (возрастающую или убывающую). Циклические колебания. Изучаемый показатель иметь циклические колебания. Эти колебания могут носить сезонный характер, поскольку деятельность определенных отраслей экономики зависит от времени квартала — времени года (например, цены на сельскохозяйственную продукцию зимой имеют минимальные значения, летом — максимальные). При наличии большого количества данных за длительные периоды времени можно выявить циклические колебания, связанные с общей динамикой рынка.

Часть временных рядов не содержат тенденции и циклической (сезонной) компоненты, а каждый следующий их уровень складывается из суммы среднего уровня ряда и некоторой случайной компоненты. Компоненты временного ряда. На практике модели временного ряда содержат три, две или одну компоненту.

Иногда фактический уровень временного ряда можно представить как сумму трендовой и циклической компоненты. Если модель определяется произведением компонент, то она называется мультипликативной моделью временного ряда. Модель, в которой временной ряд определяется суммой перечисленных компонентов, называется аддитивной моделью временного ряда.

Главная задача исследований в отдельного временного ряда, заключается в нахождении количественного значения каждой из компонент затем, чтобы использовать эту информацию для прогнозирования значений ряда или при построении моделей взаимосвязи двух, трех или более временных рядов. Источник: Эконометрика: Учебник / Под ред.